Здравствуйте, гость ( Вход | Регистрация )
  |
 29.12.2010 - 17:43 29.12.2010 - 17:43
Сообщение
#1
|
|
|
Группа: Пользователи Сообщений: 1202 Регистрация: 13.01.2008 Из: Челябинск Пользователь №: 4704 |
До лечения симптом встречался у 39 человек из 42. После лечения эти 39 человек распались на 2 группы: у которых симптом остался (12 человек) и у которых он пропал (27 человек). При этом, естественно, у кого симптома не было, он и не появился (0 человек). Эффективность лечения оцениваем критерием Мак-Немара и составляем таблицу частот до-после вида:
---------- После есть -- После нет До есть -----12 -------------27 До нет -------0 --------------3 Расчёт даёт значение хи-квадрат 27 или с поправкой Йейтса 25,037 ? колоссальная статистическая значимость. Но при этом никак не учитывается общий объём выборки. Подставим вместо 12 число 1200. Очевидно, что в данном случае препарат будет действовать уже не столь хорошо, т.к. в первом случае он помог 27 из 39 (69,2%) больных, а во втором 27 из 1227 (2,2%) больных. Однако критерий Мак-Немара даёт то же самое значение и ту же колоссальную статистическую значимость. Как-то неправильно это! Или для оценки эффективности воздействия лучше воспользоваться другими подходами? |
|
|
 |
 |
 30.12.2010 - 13:37 30.12.2010 - 13:37
Сообщение
#2
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
На мой взгляд, однозначно, да. Но меня в свое время сильно забодали здесь на форуме за мое теплое отношение к М-Н. Расширив общение, я получила программку досовскую для расчета М-Н и для таблиц более чем 2х2.
Эффективность по представленной таблице в процентах 27/42*100 и это будет 64,3% (а не 69,2% как вы посчитали). Рассуждения просты, до лечения симптом был у 39/42*100=92,9%, а после лечения симптом остался у 12/42*100=28,6%, эффективность (по этому симптому) рассматривается как разница наличия симптома до и после лечения 92,9-28,6=64,3%. Статистика критерия действительно не зависит от числа наблюдений, а только от модуля разницы b-c в четырехпольной таблице, поэтому и будет одинакова в приведенных случаях. Поэтому важно выразить эффективность как разность относительных частот с соответствующими ДИ. Для второго случая разница доли больных с симптомом до и после лечения также будет статистически значима и по критерию и по оценке ДИ разницы (95%ДИ 1,4;3,0). плав предоставил в одной из веток форума скрипт для SPSS, который выдает именно эту разность относительных частот в процентах с 95%ДИ (mn.sps). У меня есть своя самоделка для Statistica (могу прицепить), но ДИ там методом Вальда неоткорректированным, но у плава в экселевском файле есть и более корректные методы оценки ДИ. |
|
|
 |
 |
 30.12.2010 - 19:21 30.12.2010 - 19:21
Сообщение
#3
|
|
|
Группа: Пользователи Сообщений: 1202 Регистрация: 13.01.2008 Из: Челябинск Пользователь №: 4704 |
Вы снова меня выручаете! Действительно, разность долей с ДИ представляется здесь более уместной, чем Мак-Немар. К тому же интерпретация её очень прозрачная. Почитал сейчас про это в мануале StatXact 8 (стр 501, а формулы где-то выше), в ней и сделал
От души желаю Вам всего самого хорошего в наступающем году! Пользуясь случаем, также поздравляю с наступающим праздником всех модераторов, участников и гостей форума. С Новым годом! Сообщение отредактировал nokh - 30.12.2010 - 19:30 |
|
|
 |
 |
 30.12.2010 - 20:42 30.12.2010 - 20:42
Сообщение
#4
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Убрано автором
Сообщение отредактировал Игорь - 3.01.2011 - 10:59  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
 30.12.2010 - 22:47 30.12.2010 - 22:47
Сообщение
#5
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
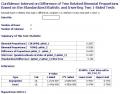
Обратите внимание на название метода, который использовал nokh
....Difference of Two Related Binomial Proportion..... А у Лапача сравнение долей в двух различных группах. А данные те, что в таблице первого поста. |
|
|
 |
 |
 30.12.2010 - 23:06 30.12.2010 - 23:06
Сообщение
#6
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Убрано автором.
Сообщение отредактировал Игорь - 3.01.2011 - 10:59  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
 1.01.2011 - 22:07 1.01.2011 - 22:07
Сообщение
#7
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Всех участников форума, а особенно, не равнодушных к статистическим проблемам поздравляю с Новым годом, желаю множества интересных задач, ни чем не ограниченного творческого вдохновения и бесконечной радости познания!
М-Н покоя не дает, а потому, продолжение темы и в новом году. Ошибка разности сомнение вызывает, .... а следовательно, и ДИ. Перепроверить бы по формулам из статьи Чубенко - благо на калькуляторе за минуту можно. Зачем же пересчитывать по Чубенко, если в документации к программе на которую ссылается nokh предоствлены и формулы и ссылки, уточню что, "формулы выше", это гл 13 Two Related Binomial Samples, которая начинается с 445 стр, и в начале главы есть ссылки на источники. ДИ, asymptotic действительно совпадает с методом Вилсона ( экселевский калькулятор плава), но в документации к 5 версии говорится, что они оставили этот расчет для преемственности с 4 версией, поскольку уже имеется более совершенный метод точной оценки (Sidik). Обратите внимание, что точный ДИ более узкий, чем по Вильсону. К сожалению у меня закончилась очередная месячная полнофункциональная демо версия StatXact, и большого опыта работы с ней у меня нет, в отличие от Statistica, но чтобы сделать вывод о ее небезупречности, такой опыт должен быть. Вы даете характеристику обеим программам, хотя по вашему признанию в глаза не видели Statistica 6, другие версии, стало быть, Вы видели "Как в Статистике 6, не знаю, т.к. не видел ее ни разу в жизни. 8.12.2010 - 18:13". Надеюсь, что StatXact, вы видели, а то получается классика "не считал, но осуждаю", а это и есть голословные суждения. Во-вторых, парность или независимость выборок имеют значение при построении таблиц. В посте-же таблица готовая. Т.о., какая разница? Разница в том, что ошибка для разности относительных частот в связанных выборках считается иначе. В формулу входит и значение b и значение c соответствующей таблицы и это не таблица сопряженности (Реброва). В данном случае с=0, а могло быть и ухудшение. Ошибку к разности b-c нужно считать не по Чубенко. В AtteStat реализован расчет ошибки к разности долей в двух различный группах, которые можно представить таблицей сопряженности. Не авторитет вам StatXact, посчитайте ошибку (для разности долей связанных групп) по Ребровой, стр 181. Но расчет самой ошибки не так уж и важен, на ней основан расчет ДИ по самому простому и распространенному методу Вальда, недостатки которого нам уже известны. По Вильсону ДИ сходится, в формулу не входит ошибка к доле в явном виде. Имеются работы, в которых рассматривается вопрос выбора метода расчета ДИ к клиническим оценкам эффективности, это очень важно для повторного контроля не только за эффективностью, но и за ухудшениями при длительных наблюдениях за пациентами одной группы. Преимущества относительно Вильсона отдавались до последнего времени методу Newcomble (1998), который реализован в скрипте под SPSS выданный плавом в одной из веток, но StatXact реализовал метод Sidik (2003), который выдается в последней строке в таблички nokh. Думаю, нет основания не доверять StatXact. Сообщение отредактировал DrgLena - 1.01.2011 - 22:30 |
|
|
 |
 |
 2.01.2011 - 10:52 2.01.2011 - 10:52
Сообщение
#8
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Убрано автором
Сообщение отредактировал Игорь - 3.01.2011 - 10:59  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
 2.01.2011 - 14:25 2.01.2011 - 14:25
Сообщение
#9
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Игорь, вы продемонстрировали удивительный антагонизм пользователя с программой Statistica и с демо и с купленной версией, это единственный случай в моем окружении. Мне тоже не все удается посчитать в AtteStat, но я отношу это к своей некомпетентности.
Все известные мне программы и калькуляторы в сети интернет дают одинаковое решение примера nokh относительно значения критерия М-Н. Но чтобы его получить, нужно правильно составить таблицу, что и сделал автор поста. Реброва поможет вам понять чем отличается таблица nokh от таблицы сопряженности к которой вы сводите решение. Как раз подстановка данных из 1-го поста дает совпадение ручного счета (по формулам Лапача) и программы StatXact, за исключением стандартной ошибки. Нет, у Вас ничего не сходится, с программой StatXact и не может сойтись, поскольку таблицу вы составили не верно. Следуя Вашему правилу "доверяй, но проверяй", проверьте, как должна быть посчитана ошибка к разности долей связанных выборок. А потом посчитайте точный ДИ по методу Sidik и поймете, что там используются совсем другие оценки. Разработчики StatXact рассчитались щедро за найденную ошибку. Учитывая бесплатность лицензии AtteStat предлагаю за каждый глюк ? бутылку пива. Я, конечно не так дотошна, как ваш знакомый, на ящик не претендую, но на пару бутылок... Сообщение отредактировал DrgLena - 2.01.2011 - 19:14 |
|
|
 |
 |
 2.01.2011 - 23:07 2.01.2011 - 23:07
Сообщение
#10
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Прошу прощения уважаемых собеседников - убрал предыдущие посты в теме, ибо, не разобравшись, сказал в них откровенную чушь, которая не представляет научного интереса грядущим посетителям форума. К счастью, не статья или монография. Большое спасибо за критику.
Теперь по существу. StatXact неверно считает ошибку и доверительные интервалы. Правильные формулы в источниках: 1. Agresti A. Categorical data analysis. - Hoboken, NJ: John Wiley & Sons, 2002. 2. Fleiss J.L., Levin B., Paik M.C. Statistical methods for rates and proportions. - New York, NY: John Wiley & Sons, 2003. (в источнике дана также упрощенная формула ошибки, сильно завышенной, выводимой StatXact). Метод введен в AtteStat. Также верные формулы у Ребровой, но к моему сожалению ссылку на нее дать не могу, т.к. в названии книги употребляется наименование конкурирующего продукта. Еще раз спасибо. Сообщение отредактировал Игорь - 3.01.2011 - 11:09  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
 3.01.2011 - 15:43 3.01.2011 - 15:43
Сообщение
#11
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Мы не раз уже выясняли, что ДИ может быть посчитан различными методами. Все они именные и плав в свое время выдал собственную программку в экселе, где введены формулы и имеются названия нескольких методов. Оснований объявлять одни правильными, другие не правильными у нас нет, используются и те и другие, в том числе и в современных программах.
Оснований считать, что StatXact не правильно считает ДИ нет. Первый ДИ посчитан по Вильсону и абсолютно совпадает с рассчитанным в программе плава. Второй посчитан так, как указано в документации, ссылка также имеется: Sidik K.Exact unconditional tests for testing non-inferiority in matched-pairs design Volume 22, Issue 2, pages 265?278, 30 January 2003 Биномиальные доверительные интервалы Доверительный интервал 95% 95%ДИ N k p 42,00% 78,45% Метод Клоппера-Пирсона Exact 42 27 64,29% 49,79% 78,78% Нормальная аппроксимация (Вальд) 49,17% 77,01% Метод Вилсона 42,36% 93,53% По распределению Пуассона (через хи2) 49,12% 77,06% Откорректированный метод Вальда StatXact в первой строке выдает точно такое же значение, по методу Вилсона 49,17 ? 77,01 Как рассчитана ошибка к разности долей также описано в документации, даже в выходной таблице указано, что под названием станд. ошибка выдана ?объединенная оценка стандартного отклонения разности долей?, да, это не та оценка, которую предлагает Реброва, но это не значит, что это не правильно. За реабилитацию StatXact, конечно, пива не получу, она в ней не нуждается . А формулы, которые приводит Реброва к недружественному Вам продукту не имеют никакого отношения, там не реализованы ни оценка ошибок к долям, ни расчет ДИ к долям, а также к OR или RR. |
|
|
 |
 |
 3.01.2011 - 16:41 3.01.2011 - 16:41
Сообщение
#12
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Мы не раз уже выясняли, что ДИ может быть посчитан различными методами. Да, эта тема обсуждалась и здесь на форуме, и в личных беседах с коллегами. И, удивительно для меня, большинство высказывалось, что расчеты нужно давать разными методами (хоть 15-тью). Влияние этого мнения заметно в некоторых модулях AtteStat. Но Вы противоречите сами себе - в StatXact только 2 метода, и оба не упоминаются в классических монографиях Agresti, Флейса и Ребровой. Оснований считать, что StatXact не правильно считает ДИ нет ... Второй посчитан так, как указано в документации, ссылка также имеется: Sidik K.Exact unconditional tests for testing non-inferiority in matched-pairs design Volume 22, Issue 2, pages 265?278, 30 January 2003 Возможно. Но проверить не удалось. Сидика торгуют за доллары. Поэтому оснований считать, что StatXact считает правильно, еще более нет. ... под названием станд. ошибка выдана ... Может, лучше под названием "стандартная ошибка" было бы выдать стандартную ошибку? ... формулы, которые приводит Реброва к недружественному Вам продукту не имеют никакого отношения, там не реализованы ни оценка ошибок к долям, ни расчет ДИ к долям, а также к OR или RR. Т.е. Вы намекаете, что методы, описанные в книге про программу STATISTICA, в самой упомянутой программе не представлены? Оригинально. Сообщение отредактировал Игорь - 3.01.2011 - 16:48  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
 3.01.2011 - 17:58 3.01.2011 - 17:58
Сообщение
#13
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Да, эта тема обсуждалась и здесь на форуме, и в личных беседах с коллегами. И, удивительно для меня, большинство высказывалось, что расчеты нужно давать разными методами (хоть 15-тью). Ну если надо, делайте все методы, может у кого то есть исторический интерес ко всем описанным в литературе методам. Мне достаточно и того что выдает StatXact, который оставил только 2 метода и объяснил почему не убрали первый. Вы же объявили их ошибочными., хотя сами сознались, что не проверяли. Но проверить не удалось. Сидика торгуют за доллары. Поэтому оснований считать, что StatXact считает правильно, еще более нет. Может, лучше под названием "стандартная ошибка" было бы выдать стандартную ошибку? А они ее и выдали. Для того чтобы это проверить не нужно доллары тратить, а всего лишь документацию почитать, ну или ссылки, которые сами предлагаете, как фундаментальные Спасибо за ссылки (благо есть под рукой вторая), формула на стр 375 перед таблицей 13.3 (3 издание). s.e.=sqrt(27-0)/42=0,12371791, что и выдает наша любимая программа Т.е. Вы намекаете, что методы, описанные в книге про программу STATISTICA, в самой упомянутой программе не представлены? Оригинально. Да, это так, но используя эти формулы я смогла сделать то что мне было нужно в той же среде Statistica. Теперь, возможно, переделаю, будет как в StatXact |
|
|
 |
 |
 3.01.2011 - 20:28 3.01.2011 - 20:28
Сообщение
#14
|
|
|
Группа: Пользователи Сообщений: 1013 Регистрация: 4.10.2006 Пользователь №: 1933 |
Да, эта тема обсуждалась и здесь на форуме, и в личных беседах с коллегами. И, удивительно для меня, большинство высказывалось, что расчеты нужно давать разными методами (хоть 15-тью). Влияние этого мнения заметно в некоторых модулях AtteStat. Но Вы противоречите сами себе - в StatXact только 2 метода, и оба не упоминаются в классических монографиях Agresti, Флейса и Ребровой. Возможно. Но проверить не удалось. Сидика торгуют за доллары. Поэтому оснований считать, что StatXact считает правильно, еще более нет. Может, лучше под названием "стандартная ошибка" было бы выдать стандартную ошибку? Т.е. Вы намекаете, что методы, описанные в книге про программу STATISTICA, в самой упомянутой программе не представлены? Оригинально. Давайте только книгу Ребровой не считать "классической монографией". Методов много по одной простой причине, ни один не является "точным" в том смысле, что обеспечивает 95% покрытие, по одной простой причине - дискретность распределения. При дискретном распределении невозможно, в ряде случаев, получить "точно" 95%ДИ. Поэтому все методы и придуманные и те, что еще будут придуманы, всегда будут являться аппроксимацией. Чем меньше количество наблюдений, тем выше вероятность того, что то, что называется 95%ДИ не будет 95%ДИ. Это не катастрофа, это надо принимать как данность. Утверждать, что какой-то метод "не верный", я бы не стал. Вопрос в том, что он делает с ошибками I и II типа. Например, нормальная аппроксимация (интервал Вальда), будет завышать вероятность ошибки I типа, а "точный" интервал Клоппера-Пирсона , будет завышать ошибку II типа. Агрести считает, что его метод является наиболее приемлемым компромиссом, но все-таки компромиссом. При большом количестве наблюдений все методы будут сходиться к одному интервалу, при небольшом - все будут не вполне "точны". Что касается, статистических программ, то надо с сожалением признать, что многие (если не все) программы не считают ДИ для долей, кстати это подвигло меня, например, написать модуль для R, который считает те же интервалы, что в упоминавшейся выше экселевской таблице - теперь использую модуль в обучении. Почему авторы статистических программ (коммерческих) игнорируют этот важный инструмент описания данных - непонятно, хотя ситуация меняется. В версии 9.2 SAS, например, появилась опция binomial (ALL) в процедуре FREQ, которая рассчитывает интервалы Вальда и Клоппера-Пирсона (как это делалось и в более ранних версиях), а также Джеффриса, Агрести-Коула и Вилсона. Детали (с формулами, см. http://support.sas.com/documentation/cdl/e...0000000660.htm) Что касается теста со ссылкой на Sidik, то тут проблема - статья не совсем о том (по крайней мере ссылка) - это тест non-inferiority для парных наблюдений, т.е. доверительные интервалы для ситуации теста Мак-Немара (плюс non-inferiority). Для знакомства можно посмотреть другую статью того же автора, доступную в сети http://www.google.ru/url?sa=t&source=w...ilA&cad=rja |
|
|
 |
 |
 4.01.2011 - 15:24 4.01.2011 - 15:24
Сообщение
#15
|
|
 Группа: Пользователи Сообщений: 1114 Регистрация: 10.04.2007 Пользователь №: 4040 |
Детали (с формулами, см. http://support.sas.com/documentation/cdl/e...0000000660.htm) Недоступен источник. Поиски информации вывели на другой форум, ссылку на который позвольте поместить здесь не как на приглашение принять в нем участие, а как на законченный комплект источников и ссылок (рассматривали аналогичную проблему, причем уже довольно давно): http://www.mathkb.com/Uwe/Forum.aspx/stat-...non-independent. Может, кому-то, как и мне, материалы полезными покажутся.  Ebsignasnan prei wissant Deiws ainat! As gijwans! Sta ast stas arwis!
|
|
|
 |
 |
  |