Здравствуйте, гость ( Вход | Регистрация )
  |
 11.11.2009 - 02:55 11.11.2009 - 02:55
Сообщение
#1
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
Народ, где можно найти толковое описание процедуры проверки данных на выбросы (статистика Кука и расстояние Махаланобиса) и влияющие наблюдения?
Сообщение отредактировал Pinus - 11.11.2009 - 02:56 |
|
|
 |
 |
 11.11.2009 - 14:58 11.11.2009 - 14:58
Сообщение
#2
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Я использую статистику критерия Граббса, если просто для выбросов. Если подходит дам подробности. Или вам для регрессии?
Сообщение отредактировал DrgLena - 11.11.2009 - 15:19 |
|
|
 |
 |
 12.11.2009 - 02:14 12.11.2009 - 02:14
Сообщение
#3
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
Мне для регрессии. В Statistica предлагается два критерия (критерий Кука и расстояние Махаланобиса). Как их рассчитывать в программе вроде бы понятно, а как и с чем сравнивать (как обычно делается при оценивании) не ясно. В книжках, которые просмотрел на этот счет, пока только общие фразы и разные субъективные подходы.
|
|
|
 |
 |
 12.11.2009 - 05:46 12.11.2009 - 05:46
Сообщение
#4
|
|
|
Группа: Пользователи Сообщений: 23 Регистрация: 24.07.2009 Пользователь №: 6183 |
Выброс (outlier) определяется отдаленностью отдельного наблюдения от основной группы данных. Согласно с Tukey, критическое значение такой отдаленности наблюдения от медианы составляет 3 раза расстояние между верхней и нижней квартилями. В случае одной переменной, наиболее распространенным графическим методом диагностики выбросов является boxplot. В случае многовариантного анализа, определение выбросов очень сложно. Например, по каким критерием считать выбросом многомерный вектор ? по значительному отклонению одной из его координат или незначительному систематическому смещению во многих координатах? Одним из возможных методов детекции выбросов в многомерном пространстве является расстояние Махаланобиса, однако необходима робастная оценка ковариационной матрицы, входящей в формулу этой статистики, а это математически очень сложно.
Для определения выбросов в линейной регрессии наиболее простым и информативным методом является визуальный анализ (?на глаз?) графика остатков и подогнанных значений (Residuals vs. Fitted values). Также можно использовать ?стьюдентизированные? остатки (studentized или crossvalidated), которые имеют распределение Стьюдента, что позволяет несложно найти критические значения. Нужно отметить, что проверку на выбросы нужно проводить после любого изменения в регрессионной модели (хотя, как правило, после трансформации зависимой переменной выбросы остаются выбросами). По поводу влияющих наблюдений (influential observations). Основная идея влияющих наблюдений ? это определение изменений регрессионных параметров при удалении одного из наблюдений из модели (leave-one-out deletion). Основоположниками метода являются Belsley, Kuh and Welsch (1980), Cook and Weisberg (1982). Нужно отметить, что влияние наблюдения на модель зависит от 2-х факторов: 1) отдаленности наблюдения от центра пространства Х (проще говоря, от среднего арифметического) и 2) абсолютной величины остатка. То есть, наибольшее влияние на регрессионную модель оказывает наблюдение с высоким ?leverage? (очень отдаленное от среднего арифметического) и с большим остатком (очень отдаленное от регрессионного гиперплана). Статистика Кука (Cook?s D) определяет изменения в регрессионных коэффициентах ?бета?, если выбросить из модели одно наблюдение. Формулу для расчета можно найти в любой книге по линейной регрессии. Расстояние Кука измеряется в терминах, так называемого, доверительного эллипса, поэтому, граничным значением для этой статистики является 50-й перцентиль статистики F (0.50, р, n-p), где p ? это количество переменных, а n- количество наблюдений. Обычно этот перцентиль находится между 0,8 и 1,0. Одно замечание к статистике Кука: ее теоретическая база (ее формула) основана на предположении о нормальном распределении ошибок в модели регрессии. Где же гарантия эффективности этой статистики при значительных отклонениях от нормальности (например, при наличии влияющих наблюдений). Выглядит довольно противоречиво ... Удачи!  Андрей
|
|
|
 |
 |
 12.11.2009 - 17:28 12.11.2009 - 17:28
Сообщение
#5
|
|
|
Группа: Пользователи Сообщений: 1202 Регистрация: 13.01.2008 Из: Челябинск Пользователь №: 4704 |
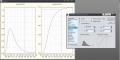
> Pinus. Посмотрел в нескольких русскоязычных книжках - тоже ничего не понравилось. В дискриминантном анализе расстояние Махаланобиса считается не для отдельных значений, а для групповых центроидов, а как? - раньше не вникал. Насколько сейчас понял из описания в википедии, геометрически расстояние Махалонобиса это - расстояние от наблюдения (на рисунке - выброс) до центроида корреляционного гипероблака r, отнесённое к его диаметру d в этом направлении. Из рисунка видно, что ни по одному признаку в отдельности выброс не обнаруживается, тогда как при одновременном учёте нескольких признаков (здесь - двух) он очевиден. Непонятно пока как рассчитывается диаметр эллипсоида, т.к. это - не есть диаметр доверительного эллипса. + само критическое значение есть величина эвристическая.
>avorotniak. Спасибо за разъяснения, стало понятнее с этими мерами. Не поясните ли ещё по поводу расчёта диаметра? Сообщение отредактировал nokh - 12.11.2009 - 17:44 |
|
|
 |
 |
 12.11.2009 - 21:50 12.11.2009 - 21:50
Сообщение
#6
|
|
|
Группа: Пользователи Сообщений: 23 Регистрация: 24.07.2009 Пользователь №: 6183 |
Сразу хотелось бы уточнить, что дистанция Махаланобиса обычно используется в многовариантном анализе (не при линейной регрессии). Это своего рода стандартизированная дистанция от вектора наблюдений до вектора средних значений (стандартизация проводится с помощью ковариационной матрицы).
Di = sqrt(t(xi - mean(x))*solve(S)*(xi ? mean(x))) Для детекции выбросов необходимо подсчитать статистику D для всех наблюдений. После чего можно предположить, что статистика D имеет распределение хи-квадрат со степенями свободы равными количеству переменных (это поможет найти критические значения). Более подробную информацию по определению выбросов в многомерном пространстве можно найти, например, в книге Methods of Multivariate Analysis ALVIN C. RENCHER (стр.101). Важно отметить, что для подсчета статистики D желательно использовать робастные оценки для положения и дисперсии-корреляции. В отношении осей указанного эллипсоида: Их направление задается собственными векторами, а длина полуосей пропорциональна соответствующим собственным значениям.  Андрей
|
|
|
 |
 |
 12.11.2009 - 22:24 12.11.2009 - 22:24
Сообщение
#7
|
|
|
Группа: Пользователи Сообщений: 1202 Регистрация: 13.01.2008 Из: Челябинск Пользователь №: 4704 |
Большое спасибо, посмотрю. Кому нужно: http://photoshopia.su/26806-methods-of-mul...-besplatno.html
|
|
|
 |
 |
 13.11.2009 - 14:24 13.11.2009 - 14:24
Сообщение
#8
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
Avorotniak, большое спасибо за ответ!
Если не затруднит, посоветуйте: 1. Регрессия простая нелинейная (полином 2-го порядка). Можно ли использовать для проверки на выбросы графический анализ (в Statistica 6 нет приведенного Вами графика Residuals vs. Fitted values, можно ли использовать Predicted vs. Residual Scores: по сути, наверно, то же самое, только оси наоборот)? Вообще, если я правильно понимаю, то суть такого графического метода заключается в нахождении данных с резко отличающимися остатками. Тогда можно использовать обычный график зависимой и независимой переменных с облаком рассеяния и линией регрессии: смотрим значения с сильно большими остатками ? расстояние от линии регрессии до значения переменной по оси Y. Тогда почему нельзя также сделать в отношении простой нелинейной регрессии (один влияющий фактор)? Когда два и более факторов, то понятно ? пространство. 2. Если графическим путем установлено нормальное распределение остатков, можно ли для полинома использовать статистику Кука (полином ? функция линеаризуемая)? Или только для простых линейных регрессий? 3. Из сказанного Вами по поводу влияющих наблюдений, можно заключить следующее: если облако рассеяния однородное (пусть даже вытянутое, но с более или менее равномерным распределением значений влияющего фактора, особенно по краям), и крайних значений не одно, а несколько, и их остатки невелики, то беспокоится о проверке влияющих наблюдений не стоит и, в принципе, графического анализа и в этом случае будет достаточно. Правильно? |
|
|
 |
 |
 13.11.2009 - 14:42 13.11.2009 - 14:42
Сообщение
#9
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
nokh, не встречали ли где про Кука? При каких условиях и при каких предпосылках применяется метод, техника получения результатов и их интерпретация? Все остальное, что для продвинутых математиков и на аглицком языке, мне пока не поднять.
|
|
|
 |
 |
 13.11.2009 - 17:37 13.11.2009 - 17:37
Сообщение
#10
|
|
|
Группа: Пользователи Сообщений: 23 Регистрация: 24.07.2009 Пользователь №: 6183 |
Вопрос:
Регрессия простая нелинейная (полином 2-го порядка). Можно ли использовать для проверки на выбросы графический анализ (в Statistica 6 нет приведенного Вами графика Residuals vs. Fitted values, можно ли использовать Predicted vs. Residual Scores: по сути, наверно, то же самое, только оси наоборот)? Вообще, если я правильно понимаю, то суть такого графического метода заключается в нахождении данных с резко отличающимися остатками. Тогда можно использовать обычный график зависимой и независимой переменных с облаком рассеяния и линией регрессии: смотрим значения с сильно большими остатками ? расстояние от линии регрессии до значения переменной по оси Y. Тогда почему нельзя также сделать в отношении простой нелинейной регрессии (один влияющий фактор)? Когда два и более факторов, то понятно ? пространство. Ответ Очень важный момент: линейность регрессии определяется ее параметрами (коэффициентами), а не переменными. Поэтому, полиномиальная регрессия все же остается линейной, со всеми вытекающими последствиями. Упомянутый Вами график Predicted vs. Residual Scores, по-видимому, является графиком стандартизированных остатков (разделенных на свое стандартное отклонение). В принципе, нет проблем, даже лучше для детекции выбросов. Обычный график зависимой и независимой переменных с облаком рассеяния и линией регрессии дает лишь приблизительное представление, так как, остатки ? это разница между наблюдением и ?рredicted? в квадрате: квадрат (y ? y fit); Вопрос: Если графическим путем установлено нормальное распределение остатков, можно ли для полинома использовать статистику Кука (полином ? функция линеаризуемая)? Или только для простых линейных регрессий? Ответ: Полиномиальная регрессия - это линейная регрессия, поэтому можете использовать статистику Кука. Кстати, для детекции влияющих наблюдений, также можете использовать DF FIT, DF BETA ? поищите в своей программе. На графике остатков основное внимание обращается на гомогенность облака, эта гомогенность свидетельствует об однородности дисперсий остатков (что тесно связано с нормальностью). Проверка на нормальность обычно проводится с помощью QQ plot. Вопрос: Из сказанного Вами по поводу влияющих наблюдений, можно заключить следующее: если облако рассеяния однородное (пусть даже вытянутое, но с более или менее равномерным распределением значений влияющего фактора, особенно по краям), и крайних значений не одно, а несколько, и их остатки невелики, то беспокоится о проверке влияющих наблюдений не стоит и, в принципе, графического анализа и в этом случае будет достаточно. Правильно? Ответ: В принципе, правильно. Однако, учитывая, что все более менее нормальные статистические программы без труда проводят регрессионную диагностику (графики остатков, определение влияющих наблюдений и многое другое), думаю, что стоит, на всякий случай, убедится или глаз нас не обманывает. Важное замечание: для оценки коэфициентов регрессии (если модель используется для предсказания) распределение остатков не очень важно, так как при разработке теории для такой оценки не используется предположение о нормальном распределении ошибок. Однако, если Вы хотите провести инференцию (найти доверительные интервалы для коэфициентов), тогда важно убедится в том, что остатки не сильно отклоняются от нормального распределения (оценка такого отклонения довольно субъективна, так как, понятие нормальности используется для разработки теорий, на практике она не существует).  Андрей
|
|
|
 |
 |
 13.11.2009 - 18:16 13.11.2009 - 18:16
Сообщение
#11
|
|
|
Группа: Пользователи Сообщений: 23 Регистрация: 24.07.2009 Пользователь №: 6183 |
Извините, небольшая поправка к следующей фразе:
Обычный график зависимой и независимой переменных с облаком рассеяния и линией регрессии дает лишь приблизительное представление, так как, остатки это разница между наблюдением и рredicted? в квадрате: квадрат (y ? y fit); Остатки это разница между наблюдением и предсказанным значением. Квадрат из другой оперы (сумма квадратов остатков).  Андрей
|
|
|
 |
 |
 14.11.2009 - 08:10 14.11.2009 - 08:10
Сообщение
#12
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
Статистика Кука (Cook?s D) определяет изменения в регрессионных коэффициентах ?бета?, если выбросить из модели одно наблюдение. Формулу для расчета можно найти в любой книге по линейной регрессии. Расстояние Кука измеряется в терминах, так называемого, доверительного эллипса, поэтому, граничным значением для этой статистики является 50-й перцентиль статистики F (0.50, р, n-p), где p ? это количество переменных, а n- количество наблюдений. Обычно этот перцентиль находится между 0,8 и 1,0. Думаю для нахождения критического значения воспользоваться таблицами Большева, Смирнова (процентные точки F-распределения). В них F(Q, v1, v2), где Q задается в процентах. Значит следует брать Q не 0,5, а 50. Я правильно понимаю? В таблице для нахождения значений функции между предложенными градациями предлагается использовать квадратичную гармоническую интерполяцию. Нет ли в распространенных программах получения точных значений F-распределения при заданных значениях процентных точек и степеней свободы? Если не затруднит, из какого источника Вы приводите такое нахождение критического значения статистики Кука? Я не могу в русских книгах по регрессионному анализу найти про критерий Кука совсем ничего. |
|
|
 |
 |
 14.11.2009 - 14:24 14.11.2009 - 14:24
Сообщение
#13
|
|
|
Группа: Пользователи Сообщений: 1325 Регистрация: 27.11.2007 Пользователь №: 4573 |
Нет ли в распространенных программах получения точных значений F-распределения при заданных значениях процентных точек и степеней свободы? Есть, в Statistica; Probability Distribution Calculator v1 и v2 в df1 и df2, а Q задается не в процентах, а в долях в окне ?p?, и ставьте метку ?invers? . |
|
|
 |
 |
 14.11.2009 - 14:28 14.11.2009 - 14:28
Сообщение
#14
|
|
|
Группа: Пользователи Сообщений: 23 Регистрация: 24.07.2009 Пользователь №: 6183 |
Правильно по поводу перцентиля 50, однако поищите в Вашем софте, должно быть.
По поводу статистики Кука и других мер для влияющих наблюдений войдите в bib.tiera.ru, введите автора Rawlings и скачайте книгу по регрессионному анализу. На странице 362 этой книги найдете все ответы на интересующие Вас ответы. Удачи! Андрей  Андрей
|
|
|
 |
 |
 15.11.2009 - 02:30 15.11.2009 - 02:30
Сообщение
#15
|
|
|
Группа: Пользователи Сообщений: 244 Регистрация: 28.08.2009 Пользователь №: 6286 |
DrgLena, спасибо!
Андрей, тоже спасибо! Скачал книгу, попробую несколько страниц перевести. |
|
|
 |
 |
  |