Поправка Бонферрони или FDR Опции

[vas]

Здравствуйте! У меня вопрос по поводу множественного сравнения. А конкретно, по поправке Бонферрони.

Как он считается? Я p делю на количество групп сравнения или на общее количество тестов? Вот допустим, у меня работа по полиморфизмам SNP, т.е есть индивиды с тремя генотипами, и они сравниваются между собой по 11 показателям. Мне делить p на 3 или на 33??? Или на 11?
И еще вопрос. Его мне применять ко всему исследованию или только к 1 полиморфизму???

Еще хотелось бы узнать преимущества FDR (False discovery rate) контроля. И про возможность его использования вместо поправки Бонферрони.

PS Читал нижний топик про тест Крускалл-Валлиса, но не совсем понял. Вот если я сравниваю три группы индивидов, и нахожу значимое различие по какому-нибудь показателю, то могу судить лишь о том, что они различаются между собой??? НО не могу, допустим, судить о том как они различаются.

Сообщение отредактировал vas - 30.09.2013 - 06:37

[anserovtv]

В поправке Бонферрони уровень значимости альфа делится на число сравнений и р-значения сравниваются с этим уменьшенным уровнем значимости.
У вас , как я понимаю содержательную часть, будет делиться на 3 (число сочетаний из 3 по 2 или (3*2)/2 ) по каждому показателю отдельно.
Обычно множественные сравнения выполняются в среде статпакетов. По моим сведениям чаще применяется метод Шеффе. Из моего опыта: все поправки дают почти всегда одинаковый результат.
Применение поправок зависит и от равенства-неравенства дисперсий.
Если равенство дисперсий не выполняется , то применяются особые поправки.
Видимо, в вашем случае лучше применять многофакторный одномерный или многофакторный многомерный дисперсионный анализ.
По непараметрическим методам: если при сравнении нескольких независимых выборок по
критерию Крускала-Уоллеса нулевая гипотеза отвергается (различия значимы),
следует провести все попарные сравнения каждой группы со всеми другими по критерию Манна-Уитни.
Также можно применять критерий направленных альтернатив Джонкира-Терпстра и другие методы.
Все попарные сравнения с поправками легко сделать в пакетах программ.

Сообщение отредактировал anserovtv - 2.10.2013 - 20:28

[anserovtv]

Вы не написали, отвергается ли нулевая гипотеза при сравнении всех групп сразу.

Сообщение отредактировал anserovtv - 1.10.2013 - 13:35

[vas]

Большое спасибо за ответ!

По Крускалл-Валлису, нулевая гипотеза отвергается по некоторым показателям.

В поправке Бонферрони уровень значимости альфа делится на число сравнений и р-значения сравниваются с этим уменьшенным уровнем значимости.
У вас , как я понимаю содержательную часть, будет делиться на 3 (число сочетаний из 3 по 2 или (3*2)/2 ) по каждому показателю отдельно.
Обычно множественные сравнения выполняются в среде статпакетов. По моим сведениям чаще применяется метод Щеффе. Из моего опыта: все поправки дают почти всегда одинаковый результат.
Применение поправок зависит и от равенства-неравенства дисперсий.
Если равенство дисперсий не выполняется , то применяются особые поправки.
Видимо, в вашем случае лучше применять многофакторный одномерный или многофакторный многомерный дисперсионный анализ.
По непараметрическим методам: если при сравнении нескольких независимых выборок по
критерию Крускала-Уоллеса нулевая гипотеза отвергается (различия значимы),
следует провести все попарные сравнения каждой группы со всеми другими по критерию Манна-Уитни.
Также можно применять критерий направленных альтернатив Джонкира-Терпстра и другие методы.

[anserovtv]

Все эти непараметрические критерии с попарными сравнениями и с поправками значимости имеются в пакете
SPSS версий 19-21 /с графической иллюстрацией!/.
Нужно использовать новые диалоговые окна и открывать средство просмотра модели.
В модели будут показаны и все попарные сравнения.
Значимые попарные различия на графе и в таблицах выделяются цветом.
Слева выбираете и (или) выделяете критерий. Внизу справа находятся окна для выбора модели.
Поправки на множественность сравнений в таблицах устроены следующим образом:
уровень значимости сохраняется (0,05) , а значимости /р-значения/ увеличиваются!!!

Сообщение отредактировал anserovtv - 2.10.2013 - 20:31

Прикрепленные файлы

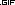 докум_2.bmp ( 1,31 мегабайт ) Кол-во скачиваний: 1047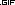
 дос2.bmp ( 2,78 мегабайт ) Кол-во скачиваний: 782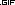
 дос3.bmp ( 3,2 мегабайт ) Кол-во скачиваний: 930

 

[vas]

anserovtv,

Большое спасибо за подробное объяснение!
И отдельное спасибо за картинки!

[p2004r]

В поправке Бонферрони уровень значимости альфа делится на число сравнений и р-значения сравниваются с этим уменьшенным уровнем значимости.
У вас , как я понимаю содержательную часть, будет делиться на 3 (число сочетаний из 3 по 2 или (3*2)/2 ) по каждому показателю отдельно.

... а потом придётся поделить и на число показателей в "ковровом бомбометании попарными сравнениями" есть хороший комикс на эту тему.

Другое дело, что метод множественного сравнения намного более разумно должен разобраться с числом степеней свободы и структурой сравнений.

[psychologist]

у меня была где то простая формула поправки бонферрони, но я её потерял. Если у меня 68 испыиуемых и 80 переменных. Напомните , полжалуйста, как мне высчитать поправку, уровень занчимости о,05.

[nokh]

у меня была где то простая формула поправки бонферрони, но я её потерял. Если у меня 68 испыиуемых и 80 переменных. Напомните , полжалуйста, как мне высчитать поправку, уровень занчимости о,05.

Это даже не формула, а дробь: сколько тестов делаете на столько и делите p. При 80 переменных парных корреляций будет: (80*80-80)/2=3160. р=0,05/3160=0,000016. При таком уровне значимости проще вообще не проводить никаких исследований, т.к. даже если значимые корреляции найдутся, ничего нового в научном плане они не принесут: столь сильные связи уже давно открыты и никому не интересны. При таком числе переменных о поправках нужно забыть. Ваш единственный выход - сворачивать пространства переменных и/или испытуемых техниками разведочного анализа, а затем тестировать малое число более осмысленных гипотез. Например, можно провести анализ главных компонент (ну или какой-нибудь любимый вариант факторного анализа, метрического шкалирования) и опираясь на результаты ординации выделить наиболее интересные направления для дальнейшего распутывания клубка связей. Хотя в любом учебнике написано, что для таких техник число объектов должно быть в 3-10 раз больше числа переменных (и, вообще говоря, об этом следует помнить планируя исследование с 80 переменными и только 68 испытуемыми!), на практике исследователи этого часто не соблюдают, т.к. результаты ординации полезны ВСЕГДА, даже если об устойчивости решения и значимости речи вообще не идёт. Далее с использованием полученных факторных меток (factor scores) в качестве новых переменных можно провести кластерный анализ и посмотреть на сколько групп схожих испытуемых разделяется выборка, что за группы и т.д.

Сообщение отредактировал nokh - 23.02.2014 - 07:06

[psychologist]

nokh, можно вас попросить пояснить почему мы 80*80 , а потом вычитаем 80?
Вот про разведочный анализ что-то слышал. Где о нем можно почитать с примерами. Метрическое шкалирование, вы имеете многомерное?
Самая главная ошибка в планирование исследований, это мало дается денег для мотивации испытуемых. Если вообще дается(

[100$]

nokh, можно вас попросить пояснить почему мы 80*80 , а потом вычитаем 80?

Потому что для к уровней фактора число попарных сравнений определяется как k(k-1)/2

Сообщение отредактировал 100$ - 24.02.2014 - 09:30

[DoctorStat]

Потому что для к уровней фактора число попарных сравнений определяется как k(k-1)/2

Это число называется биномиальным коэффициентом из k по 2.

[100$]

Это число называется биномиальным коэффициентом из k по 2.

Не то слово, доктор. Сплошная комбинаторика.

[p2004r]

> Вот про разведочный анализ что-то слышал. Где о нем можно почитать с примерами. Метрическое шкалирование, вы имеете многомерное?


Прочитайте просто справку в википедии про Анализ принципиальных(главных) компонент (PCA).

Примеры есть в любом руководстве по многомерной статистике.

[nokh]

Вот про разведочный анализ что-то слышал. Где о нем можно почитать с примерами. Метрическое шкалирование, вы имеете многомерное?

В вашем окружении обязательно должен быть человек, владеющий статистикой и многомерными техниками, т.к. без них психология давно превратилась бы из науки в то, какой она видится многим нашим акцентуированным до грани безумия практикующим психологам Лучше, чтобы первый раз технологию многомерного анализа вам показал такой человек. Даже не так важно какую: главные компоненты, факторный анализ или многомерное метрическое шкалирование (главные координаты) - с практической точки зрения они похожи; важна сама последовательность действий и интерпретация результатов. Самому осваивать будет потруднее. Посмотрите разделы по факторному анализу и многомерному шкалированию здесь: http://www.statsoft.ru/home/textbook/default.htm. Нормальные для освоения книги:
Дункан Крамер (2007) Математическая обработка данных в социальных науках. Современные методы, 2007 (есть в сети в djvu)
Наследов А.Д. (2004) Математические методы психологического исследования (даны пошаговые инструкции для пакета SPSS, есть в сети в pdf)
Наследов А.Д. (2005) SPSS. Компьютерный анализ данных в психологии и социальных науках (есть в сети в pdf)
Джонгман (1999) Анализ данных в экологии сообществ (для расширения кругозора, у экологов много интересных наработок. Есть в сети в djvu).
А примеры гуглите в сети.

Сообщение отредактировал nokh - 24.02.2014 - 17:47

[100$]

Метрическое шкалирование, вы имеете многомерное?

Псюхологист, с вашего позволения несколько уточнений косметического характера.

Ну, во-первых, никакого одномерного шкалирования и не бывает. Так что, конечно, многомерное.

Во-вторых, метрическое шкалирование Торгерсона (1952)-это исторически первая доведенная до ума техника. Однако, что в факторном анализе, что в МШ самый цимес-это возможность повращать оси полученного решения, в целях улучшения его интерпретируемости. Так что ваш случай (принимая во внимание размерность вашего признакового пространства) - это как раз НЕметрическое шкалирование Краскела (1964) и Гутмана (1968). Разумеется, размерность признакового пространства не мешало бы подскоратить. Даже проф. статпакет матрицу 80x80 может мусолить довольно долго. А потом получить вырожденное решение.
Но это, опять же, к слову. Можете не обращать внимания.

[psychologist]

как раз-таки на такие тонкости я все больше и больше стал обращать внимание.Спасибо.

[p2004r]

Разумеется, размерность признакового пространства не мешало бы подскоратить. Даже проф. статпакет матрицу 80x80 может мусолить довольно долго. А потом получить вырожденное решение.

это серьезно? даже древний StatGraph в 1988 на 286 с 1 мегабайтом ОЗУ считал 150х150 PCA

Стандартная материнка (это 16 ГБайт ОЗУ) позволяет сделать svd разложение матрицы 32000х32000. Если взять программное распределяющее (не в режиме полного копирования обращаемой матрицы) вычисление на кластер, то для редукции размерности доступны хоть пентабайтные размеры данных (сколько суммарно физической памяти есть в машинах, такой размер и можно обращать).

PS Всё это посильно для обычного исследователя.

[100$]

это серьезно? даже древний StatGraph в 1988 на 286 с 1 мегабайтом ОЗУ считал 150х150 PCA

Стандартная материнка (это 16 ГБайт ОЗУ) позволяет сделать svd разложение матрицы 32000х32000. Если взять программное распределяющее (не в режиме полного копирования обращаемой матрицы) вычисление на кластер, то для редукции размерности доступны хоть пентабайтные размеры данных (сколько суммарно физической памяти есть в машинах, такой размер и можно обращать).

PS Всё это посильно для обычного исследователя.

Это хорошие новости

[psychologist]

А если бы я высчитывал бонферрони для Анова, по такому же принципу было? 80*80-80

[100$]

А если бы я высчитывал бонферрони для Анова, по такому же принципу было? 80*80-80

Вестимо. Только многомерный ДА так топорно не делается.

[psychologist]

а какие там поправки?

[100$]

а какие там поправки?

Смысл ДА - в омнибусных тестах. ДА был придуман для того, чтобы избавиться (ну, или минимизировать, елико возможно) проблему множественных сравнений. А все эти поправки сводят проблему к тому, чего создатели ДА всячески пытались избежать.
Связи конец.

[nokh]

...Так что ваш случай (принимая во внимание размерность вашего признакового пространства) - это как раз НЕметрическое шкалирование Краскела (1964) и Гутмана (1968).

Разбирался с терминами, действительно обычно под анализом главных координат (PCoA) подразумевается классическое метрическое шкалирование, тогда как в случае использования произвольных мер сходства говорят о неметрическом шкалировании. Меня смутили авторы пакета PAST, в учебнике по которому PCoА и метрическое шкалирование указываются как синонимы.

Пока гуглил по шкалированию, наткнулся на интересный пост (http://www.papont.su/2013/03/blog-post_26.html) и не удержался от любопытства, сам проанализировал данные по гаплогруппам Y-хромосомы (http://www.eupedia.com/europe/european_y-dna_haplogroups.shtml) с использованием разных мер сходства. В очередной раз убедился, что наиболее адекватную картину дают методы, основанные на соотношении величин, а не на их абсолютных значениях. В данном случае это хорошо видно по татарам и башкирам, которые, как скоро докажут, суть - белые порубежники, охранявшие южные границы Великой Тартарии и хапнувшие южных и жёлтых кровей. У автора же блога башкиры ближе к Дании и Исландии. Ниже подшил результаты НЕметрического многомерного шкалирования и кластерного анализа (UPGMA) с использованием в качестве меры сходства корреляции Спирмена (Rho). В связи с последними событиями не перстаю удивляться насколько успешно небольшой группе носителей хищных паттернов генов троглодитов и ракшасов удаётся и дальше стравливать и дробить кластер гиперборейцев!

Сообщение отредактировал nokh - 23.03.2014 - 21:22

Эскизы прикрепленных изображений

 

[p2004r]

Пока гуглил по шкалированию, наткнулся на интересный пост (http://www.papont.su/2013/03/blog-post_26.html) и не удержался от любопытства, сам проанализировал

"Перевернутую" карту Европы я увидел у Автора блога на первом же рисунке

[100$]

А гиперборейцы - это те самые голубоглазые блондины, от которых все и произошли?

[nokh]

А гиперборейцы - это те самые голубоглазые блондины, от которых все и произошли?

Там, говорят, было больше арийских родов, чем славянских - соответственно, больше серо- и зеленогазых, чем голубо- и кареглазых. А по поводу "произошли" - нет, конечно. Как, скажем, негр может произойти от белого человека или наоборот? Эдак можно вообще договориться до того что люди от обезьян произошли А произошла только современная цивилизация, восстановилась в новом виде после последней войны с кощеями. Говорят, вся Сибирь в руинах... Потому и стравливают, что прошлого не знаем. Перефразируя одного современного политика, "сегодня в завтрашний день в прошлое не все могут смотреть, вернее смотреть могут не только лишь все, мало кто может это делать!" А современная история - лженаука, поэтому посмотрим что биологи и генетики лет через 20 скажут.
PS Если что, то ничего не курю (12 лет), не пью (скоро 7), грибы ем только съедобные, но дышу уральскими газами.

Сообщение отредактировал nokh - 25.03.2014 - 22:39

[100$]

Эдак можно вообще договориться до того что люди от обезьян произошли

Nokh, исключительно в расчете на ваше чувство юмора. Еще с советских времен:

Я книжку читал. В ней написано было,
Что предки людей - шимпанзе и горилла.
Я долго не верил, но вас повстречав,
Вдруг понял, что Дарвин был все-таки прав. (с) не помню этого шутника.

[nokh]

выучу