Критерий Манна-Уитни, и его применимость к некоторым типам данных Опции

[don]

Добрый день!
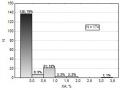
Прошу помочь в понимании следующего вопроса.
Распределение значений некоего параметра представлено на рисунке.

Видно, что большинство значений (80%) = 0.
Нужно сравнить 2 группы по данному параметру.
Вопрос: можно ли применять для сравнения критерий Манна-Уитни, учитывая, что 80% значений признака идентичны, или здесь есть некие проблемы?
В сети нашел следующую информацию
"...основное (принципиально важное) условие применимости критерия МУ: он применим ТОЛЬКО к мерным данным, т.е. таким, моделью для которых являются НЕПРЕРЫВНЫЕ случайные величины (я предпочитаю называть их "вероятностными переменными"). На практике это означает, что среди анализируемых данных не должно быть совпадающих (повторяющихся ? tied ??связанных?) значений. На практике совпадения почти неизбежны, и если их немного, то их влияние не столь заметно, и есть формулы для соответствующих поправок. Но надо знать, что при наличии совпадений критерий перестает быть свободным от распределения (непараметрическим); он начинает зависеть от неизвестной вероятности совпадений."
Товарищи, прокомментируйте пожалуйста!

Сообщение отредактировал don - 23.03.2015 - 09:11

[don]

Благодарю за ответ!
На рисунке - распределение частот аберраций в группе облученных лиц.
Я решил разбить данную выборку на 2 категории: 1) ниже референтного значения (0,2% в среднем для контрольной группы по результатам исследований) и 2) выше 0,2%
и таким образом перейти от непрерывной величины к бинарной

[nokh]

Я решил разбить данную выборку на 2 категории: 1) ниже референтного значения (0,2% в среднем для контрольной группы по результатам исследований) и 2) выше 0,2%
и таким образом перейти от непрерывной величины к бинарной

Нормально, логика в этом есть: по результатам такой таблицы можно рассчитать именно относительный риск превышения частоты ХА контрольного уровня. Мне больше нравится относительный риск - вполне понятная мера, для RR также можно рассчитать 95% ДИ - вполне современно будет. Сейчас отношения шансов толкают куда надо и не надо...

По поводу мощности не грейтесь: её всегда не хватает в Зазеркалье. А в нашем реальном мире - это уже проведённое исследование, а после драки кулаками не машут: есть именно то, что имеем. Если стоим на фриквентистских позициях - считаем р-значение, на байесовских позициях - байесовский фактор и не ноем.

Имеется 13 SNP локусов, между генотипами которых (с использованием разных генетич. моделей) планируется оценить различие в ХА.
Боюсь, что при разделении на количество групп большее чем 2, в таблицах сопряженности будет часто встречаться нулевая частота.

Если считать дедовским способами - действительно, могут быть проблемы. Если хотите серьёзную современную статистику - никакого хи-квадрата (он хуже обоснован теоретически G-критерия отношения правдоподобия) и никакого точного метода Фишера (он базируется на гипергеометрическом распределении, а в наших задачах - биномиальное или полиномиальное). Таблицы сопряжённости нужно обсчитывать точным перестановочным критерием (exact permutation test) - никаких проблем с нулевыми ячейками. Специализированная программа - StatXact от Cytel Studio, разработчики других пакетов пользуются их алгоритмами по лицензии. Кстати там же можно обсчитать таблицы с упорядоченными категориями, если там есть Манн - Уитни - можно пользоваться + их руководство полистать, оно качественное.