Анализ данных по оборачиваемости, дисперсионный анализ Опции

[maxandron]

Здравствуйте!
Нужна Ваша помощь. Анализируются данные по оборачиваемости. Для 15 аптек в течение 6 месяцев (с мая по октябрь) были получены данные по оборачиваемости (приведены в прикрепленном файле). В части аптек (аптеки 5,6,9,14) были проведены мероприятия по улучшению показателей оборачиваемости (в июне). Основная задача: анализ эффективности проведенных мероприятий (и интересно (?) вообще так ли нужны они были именно в этих аптеках). Я понимаю, что мне в данном случае может помочь дисперсионный анализ (я его задал через модуль GLM). Возникли вопросы по полученным результатам.
1) Для всей модели дисперсионного анализа получил таблицу (в прикрепленном файле). Можно ли как-нибудь оценить двухфакторное взаимодействие? Как получить значение ошибки (Error)?
2) Можно ли в моем случае вообще применять дисперсионный анализ? В прикрепленном файле находятся гистограммы распределения остатков (нормальность не видна) и результаты проверки однородности дисперсии (получил высоко статистически значимую неоднородность дисперсии в ячейках дисперсионного комплекса). На данном форуме прочитал про робастность дисперсионного анализа. Или все-таки необходимо проводить преобразование данных? Но если их провести, не потеряют ли они свой смысл (как интерпретировать изменение не оборачиваемости, а квадратного корня из значения оборачиваемости)?
3) Можно ли в данном случае и как грамотно провести Post hoc сравнения? В прикрепленном файле находятся данные, полученные при использовании теста Фишера и Тьюки для данных в моем примере ("значимых различий нет").
Может, еще что-нибудь посоветуете по анализу данных в моем примере. Заранее благодарен за ответы и помощь.

Прикрепленные файлы

 Analyse.rar ( 90,6 килобайт ) Кол-во скачиваний: 304

 

[maxandron]

Поясните, пожалуйста, что значит оборачиваемость. Это важно для интерпретации результатов. Чем она выше тем лучше или наборот?

Оборачиваемость-это количество дней в течение которых вложенные деньги в товар возвращаются организации. Поэтому, чем она ниже, тем лучше.

[nokh]

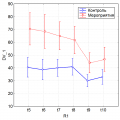
Оборачиваемость-это количество дней в течение которых вложенные деньги в товар возвращаются организации. Поэтому, чем она ниже, тем лучше.

Ну тогда всё логично получается...
Под давлением нехватки времени и прочего я близок с тому чтобы поменять своё мнение относительно выбора способа задания дисперсионного комплекса: если можно обойтись более быстрым и простым - его и использовать. Поэтому и ваш случай обсчитал не через модуль общих линейных моделей, а через модуль повторных измерений в ANOVA (хотя по объёму информации он и уступает). Для этого нужна другая организация данных: рис. прикрепил ниже. Если работать в Statistica, то в Within effects нужно проставить 6 уровней: пакет автоматически сформирует фактор повторных измерений R1, который в нашем случае означает временной фактор с 6 градациями (месяцами).
По результатам этого анализа высоко статистически значимо взаимодействие "Мероприятия х R1", что означает различие временных динамик для аптек с мероприятиями и без (контроль), т.е. различие профилей на графике. График прикрепил. Всё красиво. Видно, что это за различия в профиле: когда в контроле в период какой-то летней стагнации в контрольных аптеках всё держится на одном уровне, в аптеках с мероприятиями идёт снижение сроков оборачиваемости. В результате если до мероприятий аптеки-аутсайдеры отставали примерно (визуально) на 71-41=30, т.е. на месяц, то в октябре - уже где-то на 47-33=14 дней, т.е. на 2 недели. Я считаю, что сокращение времени оборота в 2 раза это очень хороший результат. Если нужны апостериорные сравнения - можно всё найти. В принципе, дисперсионный анализ можно было задать и как-то иначе, скажем ввести фактор "Срок" с 2 градациями: до и после мероприятий, но полагаю это только несколько усложнит анализ, а наглядности убавит.

Сообщение отредактировал nokh - 20.06.2015 - 05:46

Эскизы прикрепленных изображений

 

[p2004r]

Но почему то мне представляется более правильно считать по "нормализованному поведению", когда и матожидание и дисперсия нормированы и отличается только "форма кривой".

А что в месяце "109" случилось?

Код

> anova.onefactor(fdata(t(scale(t(data.recast[,-c(1:2)])))), data.recast[,1], plot=TRUE)

> anova.onefactor(fdata(t(scale(t(data.recast[,-c(1:2)])))), data.recast[,1], nboot=10000)$pvalue
[1] 0.0115
> anova.onefactor(fdata(t(scale(t(data.recast[,-c(1:2)])))), data.recast[,1], nboot=10000)$pvalue
[1] 0.0121
> anova.onefactor(fdata(t(scale(t(data.recast[,-c(1:2)])))), data.recast[,1], nboot=10000)$pvalue
[1] 0.0103
> anova.onefactor(fdata(t(scale(t(data.recast[,-c(1:2)])))), data.recast[,1], nboot=100000)$pvalue
[1] 0.01224

Эскизы прикрепленных изображений