Выбор методов, Mixed-effects models, непараметрические аналоги Опции

[E_VA]

Добрый день, Уважаемые участники форума!

Прошу Вашего совета с решением следующей задачи (не могу определиться с корректными методами и алгоритмами).
Пациенты разбиты на 3 группы по типу операции (50-30-30 человек), каждый характеризуется набором показателей до операции (7 шт) и они же после.
Стоят следующие задачи:
1) Сравнить показатели до и после операции в каждой группе (нужно ответить на вопрос эффективности операции и поменялся ли каждый показатель).
2) Сравнить группы до и после операции между собой по 7 показателям (нужно ответить на вопрос - есть ли среди набора показателей те, которые бы отличались в группах как до, так и после операции)
3) Разбить каждую группу на 2 подгруппы по значениям одного из 7 характеризующих их показателей (значение до какого-то балла шкалы и после) и провести сравнения для подгрупп (цель - проверка одной зарубежной статьи).

Нормальности распределений в целом нет, показатели - шкалы (0-10), (0-50) и числовые значения. Различные преобразования к нормальности тоже не приводят.
Насколько я понимаю предмет, то спотыкаюсь на проблему множественных сравнений во всей красе (вопросы 1 и 2), если сравнивать известными тестами (групповыми и парными). Надо делать корректировку на 7 показателей * 2 сравнения по времени (если сравнивать группы Краскелом-Уоллисом) + 7 показателей *3 группы (сравнение до и после в каждой группе) = 35 сравнений. И это я не затрагиваю вопрос 3.

Если смотреть рекомендации с данного форума, то основная ? дисперсионный анализ. Это вроде как Mixed-effects models. Но это было бы корректно, если бы данные были нормально распределены.
Может быть, конечно, что-то я пропустила, в этом случае буду благодарна, если отправят по нужному ?адресу?.

Единственный вариант, который благодаря p2004r пришел в голову для одновременного решения вопросов 1-2: построение деревьев классификаций при максимально возможном разбиении на группы: (время обследования + тип операции= 6 групп), а потом смотреть какие факторы позволили (и вообще позволили ли) сделать классификацию с допустимым уровнем ошибки. Потом можно объединять неразличимые группы и заново строить деревья. НО, когда задача спускается до вопроса 3, то 2*3*2=12 групп и в каждой немного данных. Сработает ли там этот подход? И будет ли это корректно? А самое главное, очень хочется врачам увидеть волшебное p.

Если есть возможность, то натолкните, пожалуйста, на корректное решение проблемы. Так как приходится использовать бесплатное ПО, то буду благодарна ссылке на функции из R.

[p2004r]

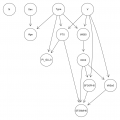
Добрый день, Уважаемые участники форума!

Единственный вариант, который благодаря p2004r пришел в голову для одновременного решения вопросов 1-2: построение деревьев классификаций при максимально возможном разбиении на группы: (время обследования + тип операции= 6 групп), а потом смотреть какие факторы позволили (и вообще позволили ли) сделать классификацию с допустимым уровнем ошибки. Потом можно объединять неразличимые группы и заново строить деревья. НО, когда задача спускается до вопроса 3, то 2*3*2=12 групп и в каждой немного данных. Сработает ли там этот подход? И будет ли это корректно? А самое главное, очень хочется врачам увидеть волшебное p.

Если есть возможность, то натолкните, пожалуйста, на корректное решение проблемы. Так как приходится использовать бесплатное ПО, то буду благодарна ссылке на функции из R.

1) Проблемы множественных групп на самом деле нет, поскольку есть чудесная техника Multi-Label Learning ( https://cran.r-project.org/web/packages/uti...ml-overview.pdf ). Это в случае когда датасет хочется рассмотреть под неким конкретным "углом зрения" и только ним.

2) Если хочется получить картину всех значимых (и что важно непротиворечивую картину) зависимостей которые следуют из датасета то есть {bnlearn}.

Например, для датасета (преобразованного в длинную форму) с которого началось обсуждение, картина вот такая получается

Код

> print(hc(datalong.bnlearn, optimized=F))

  Bayesian network learned via Score-based methods

  model:
   [N][Sex][Type][V][Age|Sex:Type][VASl0|Type:V][PT0|Type:V][ODI0|VASl0]
   [PI_GLL0|Type:PT0][SF36PH0|ODI0:V][VASs0|ODI0:V]
   [SF36MH0|ODI0:SF36PH0:VASs0:PT0]
  nodes:                                 12
  arcs:                                  17
    undirected arcs:                     0
    directed arcs:                       17
  average markov blanket size:           4.00
  average neighbourhood size:            2.83
  average branching factor:              1.42

  learning algorithm:                    Hill-Climbing
  score:                                 BIC (cond. Gauss.)
  penalization coefficient:              2.692248
  tests used in the learning procedure:  2772
  optimized:                             FALSE

V это факт воздействия оперативного Type - тип воздействия N - личность которой принадлежат замеры показателей

Вполне себе интерпретируемая картина?

Сообщение отредактировал p2004r - 7.06.2016 - 10:59

Эскизы прикрепленных изображений

 

[E_VA]

2) Если хочется получить картину всех значимых (и что важно непротиворечивую картину) зависимостей которые следуют из датасета то есть {bnlearn}.

Огромное спасибо за ссылку на {bnlearn}, произвело впечатление очень приятного и полезного инструмента. Приведенные Вами картинки имеют смысл.

1) Проблемы множественных групп на самом деле нет, поскольку есть чудесная техника Multi-Label Learning ( https://cran.r-project.org/web/packages/uti...ml-overview.pdf ). Это в случае когда датасет хочется рассмотреть под неким конкретным "углом зрения" и только ним.

Извиняюсь, если туплю. Но я пытаюсь разобраться до состояния ?сама смогу объяснить?. Поэтому у меня возник вопрос.
Насколько я поняла, пакет utiml: Utilities for multi-label learning, реализующий Multi-Label Learning, решает следующие задачи: преобразование множеств, построение подмножеств из основного множества различными способами, запускает на данных подмножествах различные методы классификации. Не совсем понимаю, как в рамках имеющегося инструмента можно отойти от проблемы множественных сравнений (формирования нескольких моделей на одном множестве). Генерировать специальным образом множества для проверки конкретных гипотез/оценки моделей?