Сравнение трёх групп с большой разницей средних Опции

[Vitek_22]

Товарищи, подсобите с анализом данных.
3 группы мышей: контроль, больные, леченные. Измерялось пройденное расстояние. Мыши с тяжёлыми двигательными нарушениями, поэтому по сравнению с контролем у них пройденное расстояние отличается на порядок. ANOVA и Tukey апостериорный показывают значимые отличия от контроля. но не между больными и леченными, хотя объективно между ними x2 разница. Интуиция подсказывает, что с такой разницей между средними сравнивать ANOVA некорректно. Но чем тогда и как это объяснить грамотно и какой критерий использовать? Если Стьюдента попарно использовать - выходит норм.

Прикрепленные файлы

 Data1.xlsx ( 9,66 килобайт ) Кол-во скачиваний: 146

 

[comisora]

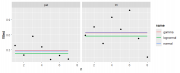
Товарищи, подсобите с анализом данных.

А почему бы не рассмотреть зависимую переменную как неотрицательную величину, пик которой будет ближе к нулю, а хвосты распределения будут говорить о самых дохлых и самых выносливых мышках? Взял три модели: нормальное распределение, логнормальное и гамма. Результаты в листинге. Отношение между контролем и лечением около 2.0-2.5 (1/0.45 - 1/0.41). Много это или мало - решать Вам, но в сравнении со здоровыми это всё очень бледно смотрится.

CODE

library(tidyverse)
library(gamlss)
dat <- readxl::read_excel('YandexDisk/Data1.xlsx') |>
mutate(across(where(is.character), ~as.factor(.))) |>
as.data.frame()
fit1 <- gamlss(value~group, data = dat, family = NO())
fit2 <- gamlss(value~group, data = dat, family = LOGNO2())
fit3 <- gamlss(value~group, data = dat, family = GAF())
df.pred <- data |>
mutate(
normal = predict(fit1, type = 'response', newdata = dat),
lognormal = predict(fit2, type = 'response', newdata = dat),
gamma = predict(fit3, type = 'response', newdata = dat)
)
perf <- performance::compare_performance(fit1,fit2,fit3)
pl <- df.pred |>
pivot_longer(cols = c(normal, lognormal, gamma), values_to = 'fitted') |>
ggplot() +
geom_line(aes(x = n, y = fitted, color = name), linewidth = 1, alpha = 0.75) +
geom_point(aes(x = n, y = value)) +
facet_grid(name~group)
posthoc1 <- pairs(emmeans::emmeans(fit1, ~group))
posthoc2 <- pairs(emmeans::emmeans(fit2, ~group, type = 'response'))
posthoc3 <- pairs(emmeans::emmeans(fit3, ~group, type = 'response'))

perf
Name | Model | AIC (weights) | AICc (weights) | BIC (weights)| Sigma
------------------------------------------------------------------------------
fit1 | gamlss | 58.3 (<.001) | 60.5 (<.001) | 62.9 (<.001) | 1.627
fit2 | gamlss | 42.2 (0.003) | 44.4 (0.006) | 46.8 (0.006) | 1.342
fit3 | gamlss | 30.7 (0.997) | 34.3 (0.994) | 36.4 (0.994) | 1.073

posthoc1
contrast estimate SE df t.ratio p.value
hc - pat 7.738 0.374 19 20.695 <.0001
hc - trt 7.362 0.361 19 20.382 <.0001
pat - trt -0.375 0.374 19 -1.004 0.5834
P value adjustment: tukey method for comparing a family of 3 estimates

posthoc2
contrast ratio SE df null z.ratio p.value
hc / pat 33.680 8.1281 Inf 1 14.573 <.0001
hc / trt 13.782 3.2133 Inf 1 11.252 <.0001
pat / trt 0.409 0.0988 Inf 1 -3.702 0.0006
P value adjustment: tukey method for comparing a family of 3 estimates
Tests are performed on the log scale

posthoc3
contrast ratio SE df null z.ratio p.value
hc / pat 27.87 6.648 Inf 1 13.948 <.0001
hc / trt 12.55 2.025 Inf 1 15.677 <.0001
pat / trt 0.45 0.123 Inf 1 -2.931 0.0095
P value adjustment: tukey method for comparing a family of 3 estimates
Tests are performed on the log scale

Эскизы прикрепленных изображений

 

Прикрепленные файлы

 Data1.xlsx ( 10,88 килобайт ) Кол-во скачиваний: 126