Сравнение трёх групп с большой разницей средних Опции

[Vitek_22]

Товарищи, подсобите с анализом данных.
3 группы мышей: контроль, больные, леченные. Измерялось пройденное расстояние. Мыши с тяжёлыми двигательными нарушениями, поэтому по сравнению с контролем у них пройденное расстояние отличается на порядок. ANOVA и Tukey апостериорный показывают значимые отличия от контроля. но не между больными и леченными, хотя объективно между ними x2 разница. Интуиция подсказывает, что с такой разницей между средними сравнивать ANOVA некорректно. Но чем тогда и как это объяснить грамотно и какой критерий использовать? Если Стьюдента попарно использовать - выходит норм.

Прикрепленные файлы

 Data1.xlsx ( 9,66 килобайт ) Кол-во скачиваний: 146

 

[nokh]

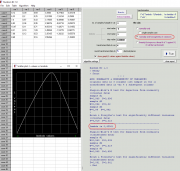
Как уже написал ИНО, требования модели дисперсионного анализа не выполняются: по критерию Левене (или как его по-русски) дисперсии неоднородны, по критерию Шапиро - Уилка остатки распределены ненормально. Прикрепил скриншоты анализа в бесплатном пакете PAST ( https://www.nhm.uio.no/english/research/resources/past/ ), который кстати в ряде моментов умеет больше чем Statistica, хотя сравнивать пакеты сложно, ввиду разных весовых категорий и назначения.

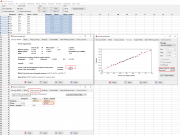
А вот с преобразованиями я бы поработал. Когда нужное преобразование неизвестно исходя из теории, можно использовать степенное преобразование Бокса - Кокса, которое приближает распределение данных к нормальному настолько, насколько позволяют сами данные. Это достигается итерационным подбором параметра лямбда. Преобразование многократно обсуждалось на форуме, но давно это было. Идея здесь такая, что мы можем либо 1) подбирать к нашим данным более подходящую статистическую модель, либо 2) преобразовать наши данные к статистической модели. Чисто философски что лучше 1) или 2) сказать нельзя, поскольку, скажем, если природа данных говорит, что площадь биологического объекта распределена ненормально, а квадратный корень из площади нормально, то естественно работать с квадратным корнем. Или если природа измеряет многие зависящие от скорости процессы скорее логарифмической линейкой, то и нам пользоваться ей естественно (скорость прямой реакции имеет ограничение варьирования слева, т.к. там зона нуля и отрицательных величин, а вправо варьировать можно: получается положительно асимметричное распределение, часто близкое к логнормальному). Для больших любителей непараметрики можно написать, что распространённые ранговые модели может и более универсальны, но не нужно забывать, что там данные тоже преобразуются, причём очень грубо - просто к порядковым местам, рангам. И если мы не видим, как такое преобразование делает статпакет для критерия Манна - Уитни или Краскела - Уоллиса, то это значит просто, что мы не считали критерии вручную и не знаем как работают эти методы. Короче, я за то, чтобы не отказываться от шкалы отношений или интервалов в пользу порядковой шкалы сразу, не попробовав менее грубые преобразования. Апостериорные сравнения по Данн в рамках Краскела - Уоллиса не находят различий между интересующими группами, хотя р близко к 0,10. Проблему можно решить добрав животных, но я против такого, если можно статистикой. Кстати, недавно узнал, что правильно не "по Данну", а по "Данн", т.к. Олив Джин Данн - женщина)) ( https://en.wikipedia.org/wiki/Olive_Jean_Dunn ) и предложила метод в статье "Multiple Comparisons Using Rank Sums" в 1964 г.

Если преобразовать сразу весь набор данных, то проблема с распределением остатков уходит, а с неоднородностью дисперсий нет. Поэтому можно использовать вариант п. Бокса - Кокса с одновременной нормализацией распределений и выравниванием дисперсий. Я умею делать такое только в очень старой программке, которую прикрепил. Она неудобная, копировать и вставлять данные из буфера получается только по одной колонке (есть такая опция в Edit), и забирать в буфер аналогично. Но она подобрала такую лямбду, что однородность дисперсий и нормальность остатков выполняются.

Теперь имеем право трактовать результаты ANOVA и проводить апостериорные сравнения. Различия между интересующими группами статистически значимы: р=0,019 по Тьюки. Лечение работает, хотя до контроля далеко, эффект "бледный" (comisora).

Сообщение отредактировал nokh - 24.09.2024 - 04:10

Эскизы прикрепленных изображений

 

Прикрепленные файлы

 Rundom_Box_Cox.zip ( 336,81 килобайт ) Кол-во скачиваний: 142