А работает ли аппарат?, ... или изгнание бесов при помощи статистики Опции

[DrgLena]

Показано конечно и очень коряво, но почему Вы не учитываете что выборки связыны?

Кто не учитывает, Юден? Он, может и не эстет, но и он и 100$ как раз связанность и анализируют.

[Диагностик]

Из их сообщений этого не следует.

[DrgLena]

Да уж, действительно забавно, не знаком ( по ссылке лень было сходить), но осуждаю этого самого Юдена с его корявыми графиками. За Юдена обидно, т.к. он уже не может сам за себя постоять. Метод описан в 1959 году, тем не менее:

This technique is now used in all measurement fields where interlaboratory agreement is important, and the term ?Youden plot? specifies not only the plotting technique but also the experimental procedure for sampling the performance of each laboratory through the results obtained on paired test items

Это как раз про корявые графики, которые я привела для участников форума, предварительно я дала ссылку на эту технику.

Аргументы 100$ статистически вполне обоснованы. Но бесы должны быть изгнаны медистами, а не статистами, если такая точность измерения им, медистам не подходит

[DoctorStat]

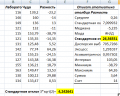
Я бы подсчитал по Вашим данным выборочную дисперсию чудо-аппарата и сравнил ее с дисперсией стандартных лабораторных измерений, которую из ваших данных получить нельзя, но она должна быть указана в спецификациях к прибору. Если дисперсии отличаются не очень сильно, то чудо работает хорошо, если дисперсия чуда много больше лабораторной дисперсии, то плохо.

Решил проделать рекомендуемый мной анализ самостоятельно. Поиск в интернете дал стандартную ошибку измерения гемоглобина с помощью спектрофотометра в районе 3 г/л. Если чудо-прибор дает аналогичную точность или лучше, то делаем, как рекомендует наш "аля Далай Лама в медицине", а именно Гланц в книге "мед-био статистика" глава "Сравнение 2-х групп. Критерий Стъюдента", параграф в этой главе "Стандартное отклонение разности". Вкратце метод сводится к следующему. Вычитаем из лабораторных показателей (первый столбец) показатели тестируемого прибора (второй столбец) и помещаем разность в третий столбец. Для з-го столбца вычисляем стандартное отклонение (=26,5 (г/л) - выделено справа желтым). Если погрешности измерений лабораторным способом и прибором приблизительно одинаковы, то стандартное отклонение разности должно быть равно (внизу выделено желтым) = s0*sqrt(2)=3*1.4=4.24 (г/л) (см.Гланца). Видно, что реальное стандартное отклонение в 26/4=6 раз больше ожидаемого. Вычислим погрешность прибора. Суммируем дисперсии: 3^2 + x^2=26,5^2 . Отсюда x=26,3 (г/л). Следовательно прибор меряет гемоглобин в 26,3/3=9 раз хуже стандарта. Выкиньте его на свалку !

Эскизы прикрепленных изображений

 

[100$]

Я исхожу из той вероятностно-статистической модели данных, что у каждого пациента в момент измерения гемоглобина есть его истинное значение (которое каждый прибор определяет с присущей ему степенью точности). Наличие в мат. модели измерения любым прибором ссылки на это самое истинное значение не позволяет считать эти измерения статистически независимыми. Оно и понятно: пациент-то один и тот же, сколькими бы приборами его не облепили.

Далее. Если взять математическое ожидание от моделей измерения, которые описаны в посте 23 (я по-прежнему утверждаю, что они кривые), то:
1. мат. ожидание измерения равно его истинному значению (иначе это не прибор, а металлолом).
2. мат. ожидание аддитивной погрешности равно нулю.
3. мат. ожидание истинного значения равно истинному значению (оно и понятно: истинное значение- детерминированная величина).
Числитель к-та корреляции представляет собой ковариацию сл. величин, т.е.: Истинное значение - Истинное значение= мат. ожидание аддитивной ошибки =0.
Иначе говоря, числитель к-та корреляции в случае зависимых (связанных выборок) равен произведению мат. ожиданий аддитивных погрешностей из обоих измерений, т. е. =0. Что нам и продемонстрировали.
Поэтому я утверждаю, что тестировать связанные выборки к-том корреляции (применительно к данной ситуации) - дурной тон.
Кроме того, известные к-ты корреляции (за исключением где-то встреченного мной параболического) линейны. А если статистическая связь двух измерений разными приборами нелинейна, то Пирсоном, Фехнером, Спирменом и Кендаллом ничего получить нельзя.

Ну и на сладкое цитатка из рускоязычной Вики:

Если X,Y независимые случайные величины, то R{X,Y} = 0. Обратное в общем случае неверно.

Сообщение отредактировал 100$ - 4.01.2015 - 22:06

[p2004r]

Кроме того, известные к-ты корреляции (за исключением где-то встреченного мной параболического) линейны. А если статистическая связь двух измерений разными приборами нелинейна, то Пирсоном, Фехнером, Спирменом и Кендаллом ничего получить нельзя.

Ну и на сладкое цитатка из рускоязычной Вики:

Если X,Y независимые случайные величины, то R{X,Y} = 0. Обратное в общем случае неверно.

позволю себе быть кратким

1. "Натягивать сову на глобус" надо уметь. Это два прибора _поверенные_ (например тупым разведением образцов (о! кстати еще один способ поверить прибор работающий с кровью вообще одним единственным образцом )) на выдачу результатов одного и того же показателя. Все погрешности "на нелинейность шкалы" _обязаны_ быть учтены конструктором прибора. Единственный ожидаемый результат это линейная зависимость показаний обоих методов.

2. R -- _выборочный_ показатель, он может быть _любым_ в пределах некоего своего _распределения_. Получить оценку этого распределения очень просто для экспериментальных данных и невероятно трудно в случае высасывания из пальцатеоретическом случае. Соответственно делать предположения о том, с какого уровня ошибки можно считать наблюдаемое достоверным событием, мы в своем (обычном повседневном) праве.

[p2004r]

без разделения fixed и random эффекта этот расчет бесполезен

[100$]

R -- _выборочный_ показатель

Золотые слова. И выборочный и теоретический. И даже известны условия, при которых выборочный сходится к теоретическому.

он может быть _любым_

Вот, поистине, бесценные сведения. Под словой "любым" , надо думать, понимается диапазон - 1 ... 1

в пределах некоего своего _распределения_

Асимптотически нормального ~N(0,1)

Получить оценку этого распределения очень просто для экспериментальных данных

Ресэмплинговыми техниками. Кто б спорил.

и невероятно трудно в случае высасывания из пальцатеоретическом случае.

Матка боска! (польск.) Ужасть-то какая! Тем не менее все это сделано.

Соответственно делать предположения о том, с какого уровня ошибки можно считать наблюдаемое достоверным событием, мы в своем (обычном повседневном) праве.

Красотища-то какая! Случайная величина в результате эксперимента (измерения гемоглобина) приняла некое численное значение. Глазам своим не верю и считаю это невозможным событием.

Неотвержение нулевой гипотезы формально не доказывает ее истинность.

Сообщение отредактировал 100$ - 5.01.2015 - 02:11

[p2004r]

Золотые слова. И выборочный и теоретический. И даже известны условия, при которых выборочный сходится к теоретическому.



Вот, поистине, бесценные сведения. Под словой "любым" , надо думать, понимается диапазон - 1 ... 1



Асимптотически нормального ~N(0,1)



Ресэмплинговыми техниками. Кто б спорил.



Матка боска! (польск.) Ужасть-то какая! Тем не менее все это сделано.



Красотища-то какая! Случайная величина в результате эксперимента (измерения гемоглобина) приняла некое численное значение. Глазам своим не верю и считаю это невозможным событием.

Неотвержение нулевой гипотезы формально не доказывает ее истинность.

1. Нако выряйте еще отдельных букв из моих слов, может из них сложится еще что то ...

Трудность отвержения отсутствия связи между измерениями "вообще" у топикстартера (как и пути её преодоления) я описал еще в первых постах этого треда.

Тем не менее, мы точно так же считаем массу событий (завтра взойдет солнце) совершенно произвольно "достоверными". В данном случае мы примем возможную ошибку выхода за границу оценки доверительного интервала как несущественную, и будем считать событие "величина находится внутри интервала" достоверным для своих дальнейших рассуждений.

Таким образом величина возможного совпадения результатов не заключена в проверке какой то там гипотезы, а в расчете величины доверительного интервала для некоторой характеристики оцениваемого прибора. И коэффициент корреляции (вернее его доверительный интервал) более чем подходит для сравнения двух приборов выдающих на гора величину в заявленных "грамм гемоглобина на объем". (было бы "много гемоглобина", "мало гемоглобина", "вся сила в гемоглобине" было бы что обсуждать ещё)

2. Асимптотически нормального ~N(0,1)

На практике данное распределение может быть каким угодно у конкретной выборки. Поэтому я пишу у "выборочного". А что там, да кабы поверьте абсолютно не интересно... так же как и рассказываемые вами неумные скетчи (над которыми я не смеялся даже когда слышал их в первый раз).

[100$]

1. Нако выряйте еще отдельных букв из моих слов, может из них сложится еще что то ...

Трудность отвержения отсутствия связи между измерениями "вообще" у топикстартера (как и пути её преодоления) я описал еще в первых постах этого треда.

Тем не менее, мы точно так же считаем массу событий (завтра взойдет солнце) совершенно произвольно "достоверными". В данном случае мы примем возможную ошибку выхода за границу оценки доверительного интервала как несущественную, и будем считать событие "величина находится внутри интервала" достоверным для своих дальнейших рассуждений.

Таким образом величина возможного совпадения результатов не заключена в проверке какой то там гипотезы, а в расчете величины доверительного интервала для некоторой характеристики оцениваемого прибора. И коэффициент корреляции (вернее его доверительный интервал) более чем подходит для сравнения двух приборов выдающих на гора величину в заявленных "грамм гемоглобина на объем". (было бы "много гемоглобина", "мало гемоглобина", "вся сила в гемоглобине" было бы что обсуждать ещё)

2. Асимптотически нормального ~N(0,1)

На практике данное распределение может быть каким угодно у конкретной выборки. Поэтому я пишу у "выборочного". А что там, да кабы поверьте абсолютно не интересно... так же как и рассказываемые вами неумные скетчи (над которыми я не смеялся даже когда слышал их в первый раз).

Ответь лучше на простенький вопрос:
1. Считаешь ли ты применительно к данному случаю два результата измерений статистически независимыми одинаково распределенным сл. величинами?

Просьба высказаться в категорях "Да-Нет". Избегая постороннего трепа.

[100$]

Да не работает этот аппарат. И отсутствие корреляции данных это очевидно показывает. Вам только одному это не понятно?

То есть взять математическое ожидание от собственной вероятностно-статистической модели измерений и подставить в формулу ковариации сл. величин ты тоже так и не смог.
Кстати, а как насчет статистической зависимости/независимости двух результатов измерений? А то что-то мы до сих пор не слыхали твоего ученого мнения.

[p2004r]

Так уже показано 27.12.2014 - 19:44

Визуализация на картинках,

Всех с Новым Годом! Мира, дружбы и любви!

а так красивее

Описание диаграммы:
http://www-pcmdi.llnl.gov/about/staff/Tayl...gram_primer.pdf

Эскизы прикрепленных изображений

 

[p2004r]

Господин Модератор!

Мне самовыпилиться с этого форума? Или как мне ещё понимать результат вашего модерирования? Как одобрение?

[nokh]

Если бы ваши данные дали бы отличный от нуля коэффициент корреляции, можно было бы пойти дальше и проверять гипотезы что в Y=eX+f, e=1, и f=0. Но поскольку этого не случилось, то делаем вывод что один из применяемых вами приборов не пригоден для дальнейшей эксплуатации. Или оба.

Целиком и полностью поддерживаю. Начинать нужно именно с корреляции, если таковой нет - всё остальное бессмысленно. Поскольку речь в постах заходила и о возможной нелинейной связи, то лучше использовать ранговую корреляцию Спирмена (или Кендалла если больше нравится). Вопреки продуцируемым некоторыми учебниками заблуждениям, ранговые корреляции измеряют также и нелинейные монотонные связи. Эту тему мы обсуждали на форуме ещё с Игорем, а он уж года 2-3 если не больше как "самовыпилился" с форума. А недавно обнаружил, что уже и в википедии это появилось: http://en.wikipedia.org/wiki/Spearman%27s_...ion_coefficient
Именно корреляция является вторым по популярности после графического метода Бланда - Альтмана (Bland-Altman plot, вот подходящий метод: http://www.medcalc.org/manual/blandaltman.php ) и, кстати, первым методом, считающим р, в медицине для установления согласия двух методов измерения: http://www.plosone.org/article/info%3Adoi%...al.pone.0037908 - см. таблицы 1-2, сама статья с детскими рассуждениями - "ни о чём". Также используется в качестве одного из инструментов для валидации методов, можно даже онлайн посчитать и нарисовать: https://www.westgard.com/mvtools.htm

Байка на тему... Сравнивали как-то результаты ЭХО-КГ и МСКТ для 4 показателей работы сердца. Так вот, 2 значимые корреляции на уровне 0,35, а две - 0,1-0,2 и незначимы. Плюс колоссальные расхождения в самих оценках, для конечносистолического объёма - просто в 2 раза. Т.к. томограф очень дорогой, ну и типа современный - браковать сей чудо-аппарат за несоответствие результатов с классикой не стали , стали разбираться. Оказалось, что различия - в настройках: томограф в автоматическом режиме усреднял показатели в движении, при ручном же анализе одного снимка результаты приблизились к классике. Это я к тому, что даже отсутствие корреляции и расхождения в оценках параметра может указывать не на непригодность прибора, а на иные причины. А вдруг чудо-аппарат работает, только для измерения "температуры в определенных точках тела" не те точки взяли, не гемоглобиновые? И вообще, особо рьяных борцов со лженаукой нужно в узде держать - во благо самой Науки!

Присоединяюсь к поздравлениям с Новым годом . Желаю всем:
(1) чтобы атмосфера дома, на работе, ну и в стране не отбивала желания заниматься любимой статистикой,
(2) чтобы ещё времени хватало!

Сообщение отредактировал nokh - 6.01.2015 - 01:47

[anserovtv]

В некоторых пакетах программ (XLStat) имеется процедура Эквивалентность тестов /TOST/, основанная на
1. вычислениях доверительных интервалов для разности значений (при выбранном уровне значимости),
2. Одновыборочных t-тестах для проверки двух направленных гипотез о равенстве разностей нижней и верхней границам ДИ.
В руководстве пользователя указана ссылка на работы Schuirman 1987.
http://www.kovcomp.co.uk/xlstat/tools/equi...-test-TOST.html
Полагаю, что для вычислений границ ДИ было бы разумно использовать и методологию ресамплинга или (и) байесовский подход.

Сообщение отредактировал anserovtv - 6.01.2015 - 12:51