Построение регрессионной модели с нелинейной зависимостью от времени, различающийся в зависимости от категориального предиктора, Кривые должны стартовать из одной точки Опции

[ИНО]

Столкнулся с проблемой. Имеются две группы животных, делая реверанс в сторону основной тематики форума, назовем их "лечение" и "контроль". В определенные дни из каждой группы отбиралось по одной особи и провождились замеры некого параметра. При этом особь изымалась безвозвратно (секир башка ), т. е. можно с легким сердцем считать, что все наблюдения независимы друг от друга. Из теоретических соображений, что в о временной точке 0, перед началом "лечения", различий между группами не было, но со временем появились. Интерес заключен в различии динамик некого параметра между "леченными" и "нелеченными".

Создадим тестовый набор данных, "приближенных к боевым":

Код

testdata<-data.frame(group=factor(c(rep("A", 7),rep("B", 6))), time=c(15, 17, 18, 19, 20, 21, 22, 15, 18, 19, 20, 21, 22), response=c(1.078, 0.949, 0.793, -2.201, -1.181, -1.95, -2.391, 2.628, 2.525, 2.852, 2.811, 3.484, 2.206))

Отобразим их на диаграмме рассеяния:

Код

plot(response~time, data=testdata, col=group, xlim=c(0,22))

Такие границы оси абсцисс выбраны, дабы нулевая временная точка уместилась, хотя вблизи нее данные собраны не были. Несмотря на малый объем выборки, различия между группами на глаз вполне явственно. Но хочется подогнать модель, которая и кривые с ДИ нарисует, и гипотезы проверит. Важное условие - кривые для обеих групп должны выходить из одной точки с абсциссой 0. Увы, я смог додуматься только до того, как этого добиться с обычной линейной регрессией:

Код

time<-seq(0, 22, 0.1)
groupA<-data.frame(group=rep(testdata$group[1], 221), time=time)
groupB<-data.frame(group=rep(testdata$group[8], 221), time=time)

predict(m1, newdata=groupA)[1]==predict(m1, newdata=groupB)[1]

TRUE

Таким образом, вышеозначенное условие выполнено: прямые выходят из одной точки. Проблема в том, что они прямые, а зависимость явно криволинейная. Поэтому пересечение по оси ординат лежит у черта на рогах:

Код

predict(m1, newdata=groupA)[1]

6.533422

На диаграмме не уместилась:

Код

lines(time, predict(m1, newdata=groupA))
lines(time, predict(m1, newdata=groupB), col="red")

См. сплошные линии на прикрепленном рисунке. Из теоретических соображений относительно изучаемого процесса, это полный нонсенс. Предположительно, истинная точка старта лежит по оси ординат где-то между 0 и 1. Я накарябал от руки пунктирные линии, которые примерно отображают характер зависимости, какой она мне видится. Увы повторить подобное с помощью, танцев вокруг lm() с полиномами и различными сплайнами не смог - кривые пересекаются где угодно, но только не в нулевой временной точке. В настоящей нелинейной регрессии типа nls() я ни в зуб ногой, да и сомнительно, что в принципе возможно определить истинный математический закон по по столь малым данным. И не нужно оно мне в принципе. Подойдут любые кривые б. м. похожие на мои пунктиры, самое главное - чтоб они плавно расходилась из нулевой временной точки, и сама эта точка отстояла по оси абсцисс не шибко далеко от интервала (0; 1). Также требуется возможность проверки гипотезы о взаимодействии фактора принадлежности группе со временем и построения ДИ для пересказанных значений.

Сообщение отредактировал ИНО - 26.04.2025 - 19:24

Эскизы прикрепленных изображений

 

[comisora]

2 ИНО

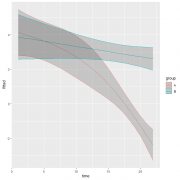
Я считаю, что нужно добавить данные в исходные моменты времени. По-хорошему, это могли быть результаты реальной секир башка в начале эксперимента в группах. По-плохому исходные данные могут быть известны из литературы. В таком случае можно попробовать взять усредненные значения, поизвлекать данные из распределений и т.д.
Наиболее научно обоснованный подход заключается в следующем: на глаз добавить значение, к которому лежит душа, в первой точке и использовать gam. Результаты на картинках.

CODE

library(tidyverse)
library(mgcv)

testdata <- data.frame(
group = factor(
c(rep("A", 8), rep("B", 7))
),
time = c(
1, 15, 17, 18, 19, 20, 21, 22,
1, 15, 18, 19, 20, 21, 22
),
response=c(
4, 1.078, 0.949, 0.793, -2.201, -1.181, -1.95, -2.391,
4, 2.628, 2.525, 2.852, 2.811, 3.484, 2.206
)
)

fit <- gam(response~group+ s(time, by = group, k = 4)+1, data = testdata)

df1 <- gratia::fitted_values(fit, gratia::data_slice(fit,
time = c(1:22),
group = gratia::evenly(group)
))

ggplot(df1, aes(x = time, y = .fitted, ymin = .lower_ci, ymax = .upper_ci,
color = group)) +
geom_line() +
geom_ribbon(alpha = 0.2)

Эскизы прикрепленных изображений

 

[ИНО]

Благодарю за проделанную работу, но это все не то. У Вас сова действительно порвалась, поскольку ордината 4 в начале - это, с позиции теоретических соображений об изучаемом процессе, полный кабздец
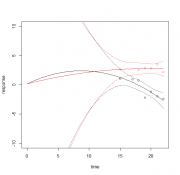
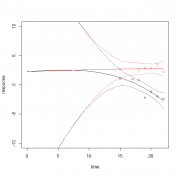
К тому же, заметьте, кривые в нулевой точки времени так и не пересеклись, хотя и близко подошли друг к дружке. А все оттого, что есть дополнительный свободный член для одной из категори:

gam(response~group+...

Не должно его быть. Добавить значение, к которому лежит душа? Тоже негоже, поскольку оно должно оцениваться моделью, пусть и с интервалом +/- лапоть за отсутствием покрытия данными в той области. Единственное в чем есть полная априорная уверенность - для обоих групп стартовые значения были равны, поскольку до начала "лечения" они принадлежали к одной генеральной совокупности. Кстати, на Вашей диаграмме доверительные интервалы в этой слепой области подозрительно узки. И уже с меньшей степенью уверенности и имеется предположение о том, какую ординату может иметь начальная точка (но явно не ту, что у Вас). В общем, что-то там не так.

Кажется, я смог решить проблему пересечения кривых в нулевой точке при помощи старой доброй lm():

Код

m2 <- lm(response~time:group+I(time^2):group,data=testdata)

Итог на рис. 1.

До этого пытался использовать функцию poly(), которая должна строить полиномы без необходимости задачи всех членов вручную и давать тот же результат, но так и не смог запрограммировать ее правильно для данного случая. Если знаете, как это сделать, прошу помощи.

Но еще больше мне понравился такой-вот недополином третей степени степени (как это вообще правильно обозвать?):

Код

m4 <- lm(response~time:group+I(time^3):group,data=testdata)

Итог на рис. 2. В отличие от рис. 1 тут кривая для группы B почти нигде не лежит над кривой для группы А, что теоретически более правильно. Ордината точки пересечения, правда, чуть не та, что я прикинул умозрительно, однако с такой шириной ДИ в данной области это неважно. И столь громадный ДИ с учетом экстраполяции почти вслепую вполне закономерен, поскольку кривая повернуть могла почти на любой угол, теоретически так и должно быть. Поэтому для проверки гипотез и подгонки кривых, хорошо аппроксимирующих процесс порождения данных в правой части диаграммы (после абcциссы 15) не было нужды добиваться пересечения в нулевой точке времени, но тут дело принципа: если мне известны строго обоснованные нестатистическими соображениями ограничения, то они обязательно должны быть наложены на модель! Теперь встает вопрос: а как собственно протестировать значимость влияния принадлежности к группе на динамику отклика в общем? anova() дает p для взаимодействий фактора группы с каждым членом полинома, а мне бы как-то обобщить...

Сообщение отредактировал ИНО - 27.04.2025 - 15:18

Эскизы прикрепленных изображений

 

[comisora]

2 ИНО

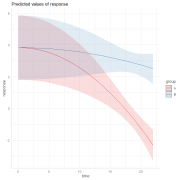
Без использования мощи библиотеки mgcv и без добавления данных на глаз можно получить такой результат (см. приложение). Метод "на глаз" почти совпал с тем, что прогнозирует текущая модель, что подтверждает его валидность . Тем не менее, мне не нравится идея подгонять модель без константы и, тем более, без наличия дополнительной информации о стартовых значениях.

CODE

testdata <- data.frame(
group = factor(
c(rep("A", 7), rep("B", 6))
),
time = c(
15, 17, 18, 19, 20, 21, 22,
15, 18, 19, 20, 21, 22
),
response=c(
1.078, 0.949, 0.793, -2.201, -1.181, -1.95, -2.391,
2.628, 2.525, 2.852, 2.811, 3.484, 2.206
)
)

fit <- lm(response~I(time^2):group,
data = testdata)
plot(ggeffects::ggpredict(fit, terms = c('time[0:22]', 'group')))

Эскизы прикрепленных изображений

 

[ИНО]

Да есть там константа, но только одна общая. Вторая - для фактора группы - лишняя, поскольку такая модель предполагает, что до "лечения" группы уже принадлежали к разным генеральным совокупностям. А это не так.

Последнюю модель я тоже рассматривал, но не удовлетворился ординатой в нулевой временной точке, не может там ее быть причине, лежащей за пределами статистики. Поэтому добавил взаимодействие фактора группы не только с квадратичным, но и с линейным членом. И получил рис.1 из предыдущего поста.

В общем, я практически удовлетворен тем, что меня вышло. Так что теперь меня мучают несколько иные вопросы, нежели заданный в стартовом посте, а именно: как это покрасивее обозвать в публикации, и каким тестом проверить гипотезу о равенстве... хм... наклонов в обеих группах.

[Диагностик]

каким тестом проверить гипотезу о равенстве...наклонов в обеих группах.

F-тест.

[ИНО]

Вопрос не в конкретном критерии, а в том как задать общий тест для линейного и квадратичного (или кубического) члена. По умолчанию anova() тестирует их отдельно. Отдельное влияние каждой инструментальной переменной неинтересно, требуется оценить взаимодействии фактора группы со временем вообще.

[ИНО]

Кажись, додумался. Надо построить две модели: одну полную, а вторую такую же, но вообще без участия фактора группы, после чего сделать anova(модель1, модель 2).

Код

m_1<-lm(response~time:group+I(time^3):group,data=testdata)
m_2<-lm(response~time+I(time^3),data=testdata)
anova(m_1, m_2)

Верно?